← back to archive

Is EAGLE-3 Speculative Decoding Lossless?

Ethan TS. Liu | January 21, 2026

EAGLE-3 (NeurIPS 2025) is the current gold standard for speculative decoding, with large speedups in SGLang and vLLM. As a brief summary, EAGLE-3's draft model fuses low, middle, and high-level features from the target model, and implements a training-time test technique to simulate multi-step generation during training.

The other day, as I was looking through their codebase, I stumbled upon something a little strange.

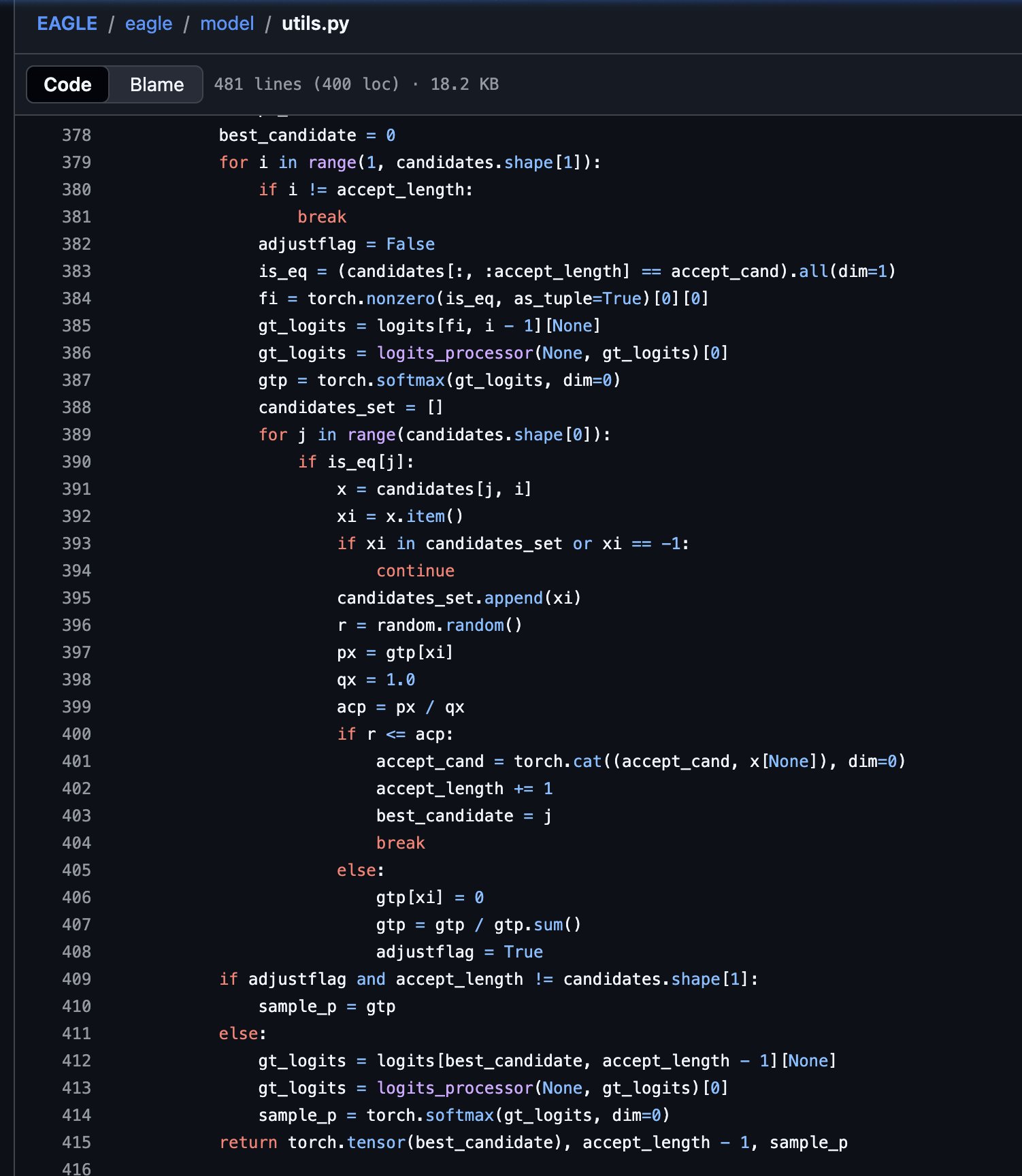
Screenshot of a code path indicating the non-greedy EAGLE-3 rejection logic.

This is their non-greedy implementation. They set \(q(x)=1\) and zero out rejected tokens in the non-greedy path, which skips the residual distribution step needed for a lossless match to \(p(x)\).

The lossless rule in speculative decoding

For non-greedy SD, when a draft proposes a token \(x\), the accept-reject rule is:

\[ \Pr[\text{accept } x] = \min\left(1, \frac{p(x)}{q(x)}\right). \]

If the proposal is rejected, the replacement token must be sampled from the residual distribution:

\[ r(x) = \mathrm{norm}(\max(0, p(x) - q(x))). \]

This residual can easily be derived by multiplying the acceptance probability by \(q(x)\), then subtracting this result from the target distribution \(p(x)\). If the reader is interested, please check out this paper.

In the current EAGLE-3 implementation, the non-greedy branch does not compute \(q(x)\) at all. Instead, it sets \(q(x) = 1\), assuming one-hot encoding and only uses the target distribution \(p(x)\) after candidate masking. So \(q(x)\) is treated as a constant, and acceptance uses \(p(x)\) directly.

This is actually lossless! This code uses \(acp = p(x)\) (since it assumes \(q(x)=1\)) and recovers by sampling from \(p\) excluding the rejected token.

In code, "resampling from a distribution excluding \(x\)" is exactly what this does: 

gtp[xi] = 0
gtp = gtp / gtp.sum()

This creates the conditional distribution \(P(k \mid k \ne x)\). When the code later calls torch.multinomial(gtp, 1), it draws from that adjusted distribution.

The probability of outputting token \(k\) under this implementation is:

\[ P(\text{output } k) = q(k)p(k) + \sum_{j \ne k} q(j)(1-p(j)) \frac{p(k)}{1-p(j)} = q(k)p(k) + \sum_{j \ne k} q(j)p(k). \]

Here \(j\) is the rejected draft token (\(j \ne k\)). The \((1-p(j))\) terms cancel, so each summand becomes \(q(j)p(k)\).

\[ P(\text{output } k) = q(k)p(k) + p(k)\sum_{j \ne k} q(j) = p(k). \]

However, even though the distribution is correct, the efficiency is terrible. In the standard algorithm, if \(p(x)=q(x)=0.1\), you accept 100% of the time. In this code, you accept only 10% of the time and resample 90% of the time for no reason.

References and discussion